Chess game - adding features

In this section, we are going to add features to our chess application. In the process, we will evaluate the maintainability of state machine modelization. The new features will also allow us to illustrate how using compound control states decreases the size of our modelized graphs.

New features’ specifications

We will add an info area which will indicate:

the player who must play next
a status message indicating whether the game is ongoing, or over

We will also add an action area with:

a undo button which will return the game to the state it was in the previous move

Follows some screens sample of the application in different states:

Initial screen	Black turn

White turn - piece selected	White wins

Modification targets

Remember that the functional design of Kingly encourages implementing a user interface with three modules with non-overlapping concerns:

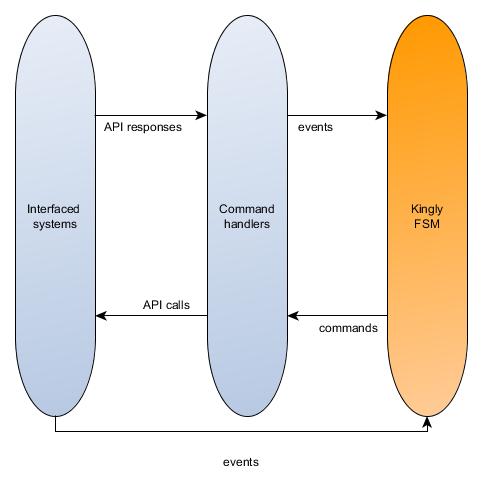
kingly-favoured ui architecture

The interfaced systems, including the input device (e.g. your laptop or mobile phone), send events to the Kingly machine. The machine computes commands which are executed by command handlers. Those commands may result in API calls on the interfaced systems, whose responses may be processed by the command handler module which in turn decides whether to send an event back to the machine for processing. This is the architecture that is implemented through the react-state-driven library for use within the React ecosystem.

As such, modifying our current chess game implementation potentially implies modifying all, some, or none of the three modules.

We will examine these modules one by one and see how adding the new features impact the current code. Let’s start with the machine.

The machine

A modification of the machine behavior is a modification of the parameters of its factory function, namely:

states
events
initial control state
initial extended state
transitions
- guards
- action factories
  - extended state updates
  - commands

The first two added features do not modify the control flow of the machine (i.e. the transitions of the machine). Instead, they involve displaying additional information. The impact thus is limited to the rendering command, which may extend to an impact on the action factories producing those commands. Those factories themselves takes as parameter the extended state of the machine and the triggering event. The two new features add no new events, hence we are left with examining the possible modifications of the extended state of the machine. To summarize, the impact is limited to all rendering commands, action factories producing rendering commands, and the extended state of the machine.

The undo feature introduces a new Undo event, corresponding to the new undo button. The new behavior can be described as follows:

in the absence of undo click, the machine behaves as before
when the user clicks on undo:
- if the machine was in the White plays or White piece selected control state, then it should move to the Black plays control state, its extended state should be the one it had before the move, and the last executed command on the interfaced systems (here the chess engine) should be reversed
- if the machine was in the Black plays or Black piece selected control state, then it should move to the White plays control state, its extended state should be the one it had before the move, and the last executed command on the interfaced systems (here the chess engine and the output device — the screen) should be reversed
- all the previous being true obviously if there was a move to undo in the first place

This gives us the following modelization:

⊕

The modifications performed on the machine are emphasized in red. Rendering commands are not represented for the sake of readability.

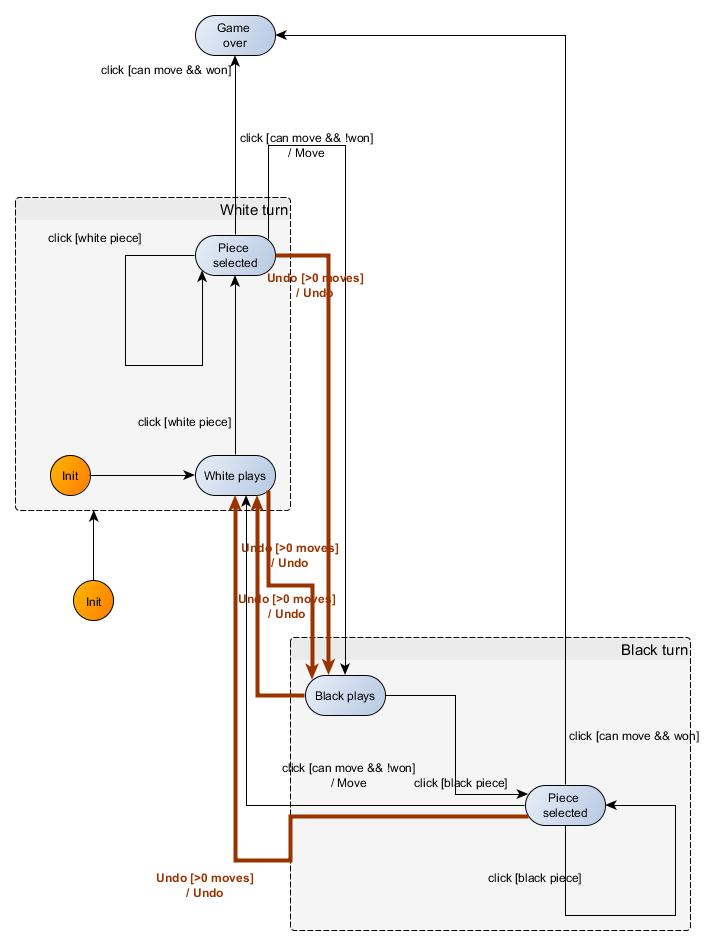
It turns out that we can simplify our graph. The Black plays and Black piece selected are the totality of the control states of the compound state Black turn. We are going to factor the arrows leaving the two black atomic states into a unique one, linking the Black turn control state, and the common target control state White plays. We naturally do the same for whites, and the modelization becomes:

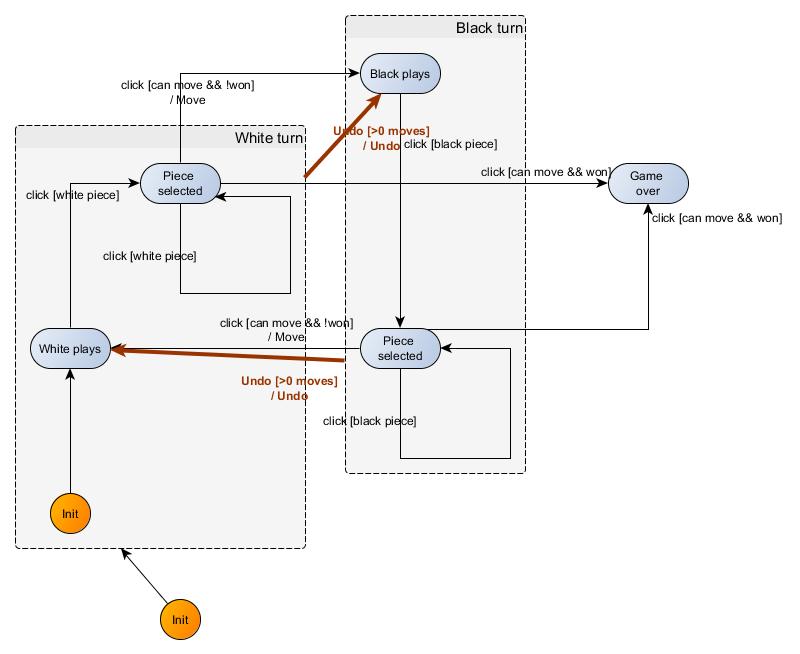
If that helps, you can think about it as an application of the good old distributivity law $ab + ac = a(b+c)$ with convenient definitions of addition and multiplication operations. The bottom line is that we simplified our graph by reducing the number of edges (transitions) between nodes (control states).

Why is that a good thing? First of all, this helps visualization. Having fewer edges to draw gives a clearer graph, which is important to communicate our design. Communicate our design in turn is important to evolve and maintain it. Maintaining 4 edges instead of 2 is more error-prone. Additionally, provided our compound states have some meaning, it reformulates more concisely the behavior! That helps to avoid errors (say you had 5 control states in the Black turn and you forgot to wire one) and finding errors in our machine design (it would be weird if one control state would go to White piece selected instead of White plays).

There is a last dimension to that. You could have for instance started your design in a top-down manner by identifying the White turn and Black turn control states, arriving first to this modelization:

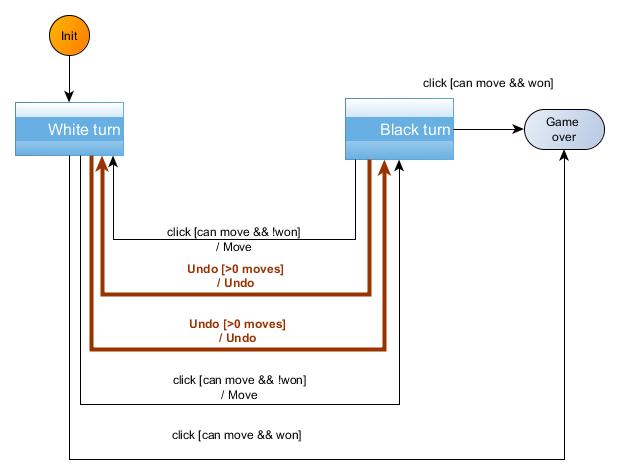
This modelization is correct and complete, but less detailed. For instance, if in the White turn atomic control state, we have a Click event, and that somehow indicates a valid move which is not final, then we should indeed go to the Black turn atomic state. Our more detailed designed explicits the somehow by introducing a second inner state for when a piece has already been clicked. This process by which an atomic state becomes a compound state by introducing sub-states is called refinement. We will not say more about this at the moment. This will be the object of a separate tutorial dedicated to modelization techniques. It suffices, for now, to understand that modeling can be an iterative top-down process by which control states are identified and then refined till a sufficient level of details is reached.

Back to the subject matter of eliciting targets for modification to implement the new features, we have finished identifying the impact of the undo feature on the machine graph. We have a new event for the machine to process. The new transitions will come with new guards and action factories. The action factories should update the extended state of the machine so that it is reversed to its previous value, and produce a new Undo command to update the chess engine which implements the game logic. The extended state of the machine may have to be augmented to keep a history of previous moves — that would impact the Move action factories related.

As a conclusion, as a result of the new features, we need to review all rendering commands, the action factories producing these commands, the extended state of the machine (adding properties to discriminate the player turn and the game status, and keeping a history of previous states), and add two new transitions.

The updated machine is as follows:

⊕

We reproduce here only the changes to the state machine. The full history of changes (rendering commands, action factories, etc.) can be observed by comparing it with the code playground from the previous implementation. At the machine level, the changes are the introduction of a new Undo event, two new properties to the extended state, and two new transitions.

const events = [UNDO, BOARD_CLICKED, START];

const initialExtendedState = {
  (...)
  status: "",
  turn: IS_WHITE_TURN,
};

const transitions = [
  (...)
  {
    from: WHITE_TURN, event: UNDO, guards: [
      { predicate: isMoveHistoryNotEmpty, to: BLACK_PLAYS, action: undoMove },
    ]
  },
  {
    from: BLACK_TURN, event: UNDO, guards: [
      { predicate: isMoveHistoryNotEmpty, to: WHITE_PLAYS, action: undoMove },
    ]
  },
];

Interfaced systems

The interfaced systems are two: the chess engine, and the output device (screen).

The chess engine need not change, as it already has all the necessary API to perform the required tasks. Concretely, the chess engine exposes an .undo API which undoes the latest move. This is thanks to the great API design of the chess engine which has included features covering all the foreseen use cases for the chess engine.

The screens produced by our application must however be updated so that an event listener is added to the Undo button and propagate its click event to the state machine. The component which renders the UI also need to change. Concretely, we now use a ChessBoardWithInfo React component:

⊕

We add two new components InfoArea and ActionArea to handle the display of the player turn and game status and the undo button. Unlike previously where we did not have control of the ChessBoard component, we can use the next props which is injected by the <Machine> component from the react-state-driven library to pass events to the machine.

function InfoArea(props) {
  const { status, turn } = props;
  console.log(`status`, status, props)
  const bgColor = turn === IS_WHITE_TURN ? 'white' : 'black';
  return div(".game-info", [
    div(".turn", [strong("Turn")]),
    div("#player-turn-box", { style: { 'backgroundColor': bgColor } }, []),
    div(".game-status", [status])
  ])
}

function ActionArea(props) {
  const {next} = props;
  return figure({onClick : ev => next({UNDO: void 0})}, [
    img(".undo", { src: "https://img.icons8.com/carbon-copy/52/000000/undo.png", alt: "undo" }),
    figcaption([
      strong("Undo")
    ])
  ])
}

function ChessBoardWithInfo(props) {
  console.log(`props`, props)
  const { draggable, width, position, boardStyle, squareStyles, onSquareClick, turn, status, undo, next } = props;
  const chessBoardProps = { draggable, width, position, boardStyle, squareStyles, onSquareClick, undo };
  const infoAreaProps = { turn, status };
  const actionAreaProps = {next};

  console.info(`chessBoardProps`, position);

  return div(".game", [
    div(".game-board", [
      h(Chessboard, chessBoardProps)
    ]),
    h(InfoArea, infoAreaProps),
    h(ActionArea, actionAreaProps)
  ])
}

export default ChessBoardWithInfo

Command handlers

We had two commands in the basic version of the chess game: Render and Move. We now have the new Undo command. Executing this command simply means executing the .undo API of the chess engine:

commandHandlers: {
  (...)
  UNDO_MOVE: function (next, _, effectHandlers) {
    const { chessEngine } = effectHandlers;
    chessEngine.undo();
  }
},

Altogether now

The previously presented pieces are glued together by the <Machine> component. The corresponding implementation can be reviewed here:

Comparing with a non-state-machine implementation

So we did this with state machines. But how would it be if we would implement the same application the usual way with React? Let’s have a look at this chess game demo, which we used as inspiration and has the same interface logic:

alternative chess demo

Thereafter follows a summary of the click event handler:

handleClick(i){
    (...)
    if(this.state.sourceSelection === -1){
      if(!squares[i] || squares[i].player !== this.state.player){
        this.setState(...);
        if (squares[i]) {
          squares[i].style = {...squares[i].style, backgroundColor: ""};
        }
      }
      else{
        squares[i].style = {...squares[i].style, backgroundColor: "RGB(111,143,114)"}; // Emerald from http://omgchess.blogspot.com/2015/09/chess-board-color-schemes.html
        this.setState(...);
      }
    }
    else if(this.state.sourceSelection > -1){
      squares[this.state.sourceSelection].style = {...squares[this.state.sourceSelection].style, backgroundColor: ""};
      if(squares[i] && squares[i].player === this.state.player){
        this.setState(...);
      }
      else{
        (...)
        if(isMovePossible && isMoveLegal){
          if(squares[i] !== null){
            if(squares[i].player === 1){
              whiteFallenSoldiers.push(squares[i]);
            }
            else{
              blackFallenSoldiers.push(squares[i]);
            }
          }
          squares[i] = squares[this.state.sourceSelection];
          squares[this.state.sourceSelection] = null;
          let player = this.state.player === 1? 2: 1;
          let turn = this.state.turn === 'white'? 'black' : 'white';
          this.setState(...);
        }
        else{
          this.setState(...);
        }
      }
    }
  }

Can you tell at a glance the logic that the click handler implemented?

We see branches, but it is not immediate how they relate to the interface specification. This problem could be remediated somewhat with a refactoring following the clean code principles. For instance, the first branch if(this.state.sourceSelection === -1) would become if (isPieceSelected). Applying this in every if .. else construct would then help figure out the logic.

When that is done, a second problem remains: there are still many branches. The cyclomatic complexity is 14! A high cyclomatic complexity correlates positively with the density of bugs. This comes from the fact that maintaining and updating logic in a code section with 14 branches is error-prone. How would you go about adding an undo feature? Which branch(es) do you modify? Do you modify any in the first place? If you do, how can you be sure that you are not breaking other features? It is hard to tell both quickly and accurately.

In comparison, the control flow implemented by the if branches is immediately visible in our state machine. The behavior of the interface is understandable quickly without reaching for the code. That speed is achieved because targeted visualizations can help our brain process information much faster than the equivalent text representation — that is why we use graphs instead of data tables, images instead of words, maps instead of text instructions.

The machine’s visualization shows in detail the control flow corresponding to the interface behavior while displaying the other details (state updates, rendering) with low fidelity (only action names). The visualization however does not loose semantics: the corresponding visual language semantics are defined to be as accurate as the equivalent textual languages.

As a matter of fact, Kingly comes with a compiler that converts from the visualization language into the JavaScript textual language (we could compile to Zig, Rust, or Swift as easily). Alternatively, as we did here, developers can encode the graph in a JSON data structure, and run the createStateMachine factory to generate an executable version of the machine. Either way, as the translation process is automated, developers cannot mess the implementation of the interface behavior. If the graph is correct (i.e. translates accurately the target specifications), and the compiler/machine factory is correct, the executable machine will also be.

Because of the equivalence between the machine’s visualization and its implementation, the visualization can become the source of truth for the interface behavior. That source of truth thus serves as a living documentation of the interface behavior.

What we learned

We learned a lot in this section.

Compound states introduce a hierarchy of states which helps to hide complexity (the sub-states in the compound state) behind an abstraction layer (the compound state). In the bottom-up design process we followed, we reached a graph with 7 control states, which gives a detailed vision of the chess application behavior. We also showed how a high-level graph, with only 3 states, can be automatically obtained by simply hiding the content of the compound states. Both visions have their value, and hierarchical state machines allow us to go back and forth between different levels of details seamlessly.

Furthermore, we showed that compound states allow the designer to simplify the visualization of a model by substituting $n$ transitions by one transition when some conditions apply. That economy is desirable as it helps control the growing complexity that characterizes an iterative development process.

We compared our machine-based interface implementation with a standard implementation and outlined that our implementation facilitates the maintainability of the application. It is easier and faster to understand the behavior as a result of the visualization of the design, and the separation of concerns realized when breaking down the behavior in control states, separating logic from effects, and using single-concern functions: guards, action factories, command handlers.

We are also decreasing the surface area of bugs, as an executable version of the machine is generated by Kingly from the machine definition. Provided that Kingly itself is bug-free (!), the produced machine (i.e. function) is guaranteed to follow the specified definition.

Additionally, our behavior model implemented by the machine serves as a living documentation of the specifications of the application’s behavior.

Exercises

The following exercises should help you check your understanding:

It would be nice to display the pieces as they are captured in the game. How would you add the feature? HINT: the ChessBoard React component has a prop to that effect.
We can improve on the info area by adding a message when a player is checked. Can you add the feature? HINT: the chess engine exposes the .in_check API to test the condition.
We can improve on the info area by adding a message when the player attempts to make an invalid move. Do you see how to do it?
The current specification do not allow for undo operations once the game is over. Can you change that so a player can undo also when the game is ended?

← Two-player chess game Chess game - more features →

Tutorials

Introduction

Counter

Password meter

Chess game

RealWorld clone

Chess game - adding features

New features’ specifications

Modification targets

The machine

Interfaced systems

Command handlers

Altogether now

Comparing with a non-state-machine implementation

What we learned

Exercises

Tutorials 1.0

Introduction

Counter

Password meter

Chess game

RealWorld clone

Chess game - adding features

New features’ specifications

Modification targets

The machine

Interfaced systems

Command handlers

Altogether now

Comparing with a non-state-machine implementation

What we learned

Exercises

Tutorials